Eksamensoppgaver med løsningsforslag

Løsningsforslag eksamensoppgave i mikroøkonomi ved HiMolde våren 2005

Dette er egentlig ikke et løsningsforslag, men en sensorveiledning skrevet til Anders Dedekam jr.

Oppgave 1 (Vekt: 50 %)

Oppgavetekst

Denne oppgaven tar for seg markedet for bilbensin. Du har følgende opplysninger som du skal bruke til å besvare spørsmålene under: Den årlige omsetningen av bensin er på om lag 2 milliarder liter. Produsentenes grensekostnader er uavhengig produksjonsnivå, og antas å være på kr. 4,00 pr. liter bensin. Avgiftene til staten (særavgift pluss merverdiavgift) er kr. 7,00 pr. liter. Videre antar vi at etterspørselens egenpriselastisitet (Cournot-elastisiteten) er 0,1 i absoluttverdi.

a) Drøft kort hvorvidt du mener at antagelsene som er gitt rundt tilbuds- og etterspørselsforholdene virker rimelige. Illustrer markedslikevekten grafisk.

b) Hvem er det som bærer byrden av denne avgiften? Argumenter.

I dagens samfunn trenger staten inntekter, og avgiften på bensin er én mulig måte til å skaffe seg inntekter på.

c) Diskuter ut i fra samfunnsøkonomiske effektivitetshensyn hvorvidt dette markedet, slik det fremkommer av opplysningene over, er egnet som inntektskilde for staten.

Et annet argument for å skattlegge bilbensin er at konsumentene som bruker bensin påfører samfunnet kostnader som de ellers ikke betaler for (eksterne kostnader). Blant annet så vil bilbruk innebære kostnader ved veislitasje, miljøkostnader og ulykkeskostnader. La oss anta at disse kostnadene til sammen utgjør 12 milliarder kroner.

d) Finn ut hva avgiftsbeløpet pr. liter bensin skal være dersom myndighetenes mål er å få inn 12 milliarder, slik at konsumentene dekker de samfunnsøkonomiske kostnadene ved bilbruk.

Det er klart at det er knyttet usikkerhet til anslaget på 12 milliarder i eksterne kostnader. En del økonomer mener nok også at dette beløpet er altfor lavt, og at 50 milliarder er et mer rimelig anslag.

e) Gi et anslag på hvor stor avgiften må være dersom myndigheten skal ta inn 50 milliarder i inntekter.

En annen måte staten kunne fått inn 50 milliarder på er å skattelegge inntekten. La oss anta at denne skatten er en fast stykkskatt på inntekt (lump sum skatt). Anta videre at alle som har inntekt bruker bil.

f) Hvilket skattealternativ (avgift på bensin eller en fast skatt på inntekt) ville du ha foretrukket som konsument? Hvilket skattealternativ ville du foreslått dersom du var rådgiver for regjeringen? Bruk relevante modeller i din argumentasjon.

Løsningsforsalg

a) Ifølge oppgaven er tilbudsfunksjonen perfekt elastisk. Dette betyr at kostnaden ved å produsere én ekstra enhet er lik for alle enheter. På kort sikt er vel dette en rimelig antagelse dersom man tenker seg at det er råolje som i all hovedsak er den variable innsatsfaktoren, og at man ikke opererer på kapasitetsskranken. (Arbeid blir vel her å betrakte som en fast innsatsfaktor: om man skal produsere 1 mill. liter eller 2 mill. liter så er det de samme knappene å ”skru” på, man trenger ikke flere arbeidere.)

Etterspørselen er uelastisk, og i oppgaven oppgitt til å være 0,1 i absoluttverdi, noe som betyr at en økning i pris på 1 % reduserer etterspørselen med 0,1 %. Virkningen av en endring i (egen)pris har to effekter, substitusjonseffekt og inntektseffekt. Jeg så for meg følgende mulige forklaring (det kan vel også være andre): få gode substitutter til bensin gir at substitusjonseffekten er liten, samt at det er et nødvendighetsgode (dette kan vel variere for ulike typer bilbrukere, produsenter, etc.).

Poenget med en slik oppgave er vel ikke hvorvidt du er enig eller ikke i antagelsene rundt tilbud og etterspørselsfunksjonen, men at argumentasjonen er noenlunde plausibel.

Figuren ser omtrent slik ut:

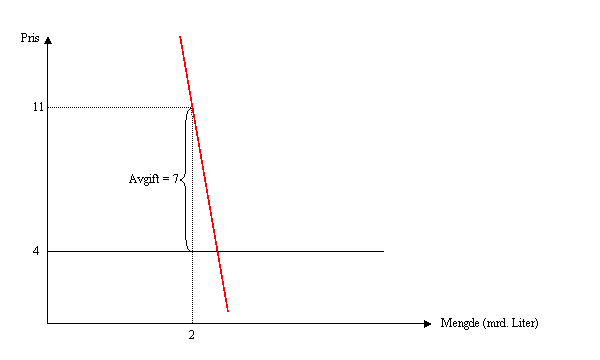
b) Jfr. Daltons sats, så er det konsumentene som bærer hele byrden av en avgift på 7 kroner, siden tilbudskurven er perfekt elastisk.

c) Siden etterspørselens egenpriselastisitet (Cournot-elastisiteten) er lav så vil avgiften føre til et forholdsvis beskjedent samfunnsøkonomisk velferdstap (Se figur: etterspørselskurven som er markert i blått har en høyere elastisitet og her er det samfunnsøkonomiske effektivitetstapet større).

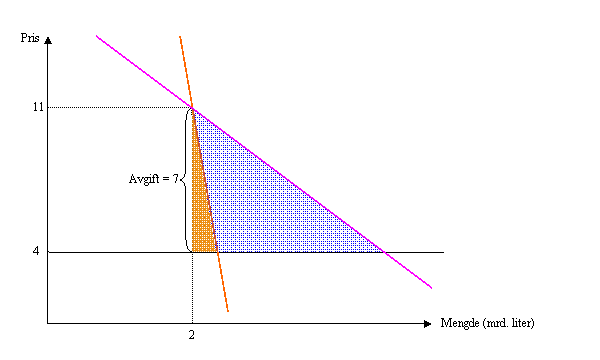
(Ser for meg at en del studenter kommer til å blande sammen effektivitetshensyn med hvem som bærer byrden av avgiften.)

d) Avgiften i dag gir en inntekt på 7*2 = 14 mrd kroner. Altså: statens inntekt skal ned med 2 mrd. Tipper at de fleste kommer med at avgiften må ned til 6 kroner, noe som jeg synes blir litt upresist dersom de ikke begrunner det med at etterspørselskurven er uelastisk slik at mengdeeffekten er beskjeden.

For å komme noe mer videre må man forutsette at etterspørselen er lineær. Videre så vet vi at det er konsumentene som bærer hele avgiften slik at en endring i avgiften er lik en tilsvarende endring i konsumentpris. Ved litt regning kommer man frem til at:

der I = statens inntekt, A = avgift, ε = egenpriselastisiteten og X = mengde. Da har vi:

Altså, prisen skal ned litt mindre enn en krone. Årsaken er at prisnedgangen gir en ”beskjeden” positiv mengdeeffekt.

e) Her får vi en økning i avgiften på 50-14=36 mrd. Ved å bruke samme formel finner vi at:

Dette impliserer en bensinpris på omtrent 26,46 (15,46 +4 +7), som er noe høyere enn standardsvaret til studentene som skriver at bensinprisen må bli 25. Så lenge de argumenterer med uelastisk etterspørsel (og dermed liten mengde effekt) synes jeg det er ok.

f) Som konsument ønsker jeg meg en lump sum skatt. Årsak: det gir ingen substitusjonseffekt (se fig under: rød figur illustrerer effekt av økt pris på bensin, blå figur illustrerer en tilsvarende lump sum skatt og nyttenivået er høyest ved lump sum).

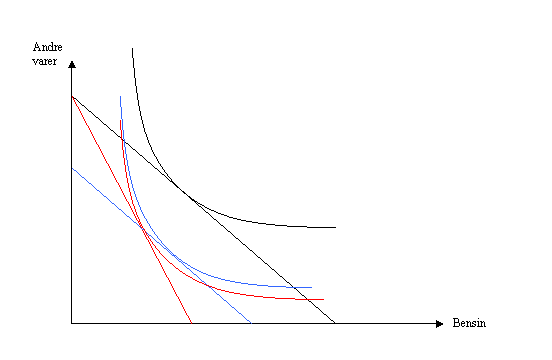
Når det gjelder hvilket skattealternativ som ville blitt foreslått som rådgiver for regjeringen, så lister jeg opp noen momenter:

· en avgift på bensin er lite egnet for å få ned forbruket, siden elastisiteten er lav.

· det samfunnsøkonomiske tapet lite ved en avgift på bensin, delvis av samme grunn.

· Hvor stor er de administrative kostnadene ved de to forslagene?

· Dersom skatten/avgiften skal dekke inn for negative eksterne effekten ved bilbruk så kan det være fornuftig å skattlegge de som påfører den negative eksterne effekten.

Her er sikkert mer, men jeg haster videre til neste oppgave.

Oppgave 2 (Vekt: 25 %)

Oppgavetekst

Et forslag som har vært diskutert i media den siste tiden er innføring av seks timers dagen. Anta at tilbudet av arbeidskraft er perfekt uelastisk. Bruk relevante modeller til å svare på følgende spørsmål:

a) Diskuter hvordan et slikt forslag vil virke inn på markedet for arbeid.

b) Hvordan vil et slikt forslag virke inn på bedriftenes avveiing når det gjelder optimal bruk av innsatsfaktorer.

Løsningsforslag

a) En innføring av 6-timers-dagen fører til at hver arbeidstaker da vil tilby 6 timer i stedet for 7,5 timer. Med ca. 2 mill. arbeidstakere så vil tilbudet falle fra 2mill*7,5= 15 mill timer hver dag til 12 mill arbeidstimer hver dag. Det er antatt i oppgaven at tilbudet av arbeid er perfekt uelastisk, etterspørselen antar vi er fallende. Vi får følgende figur:

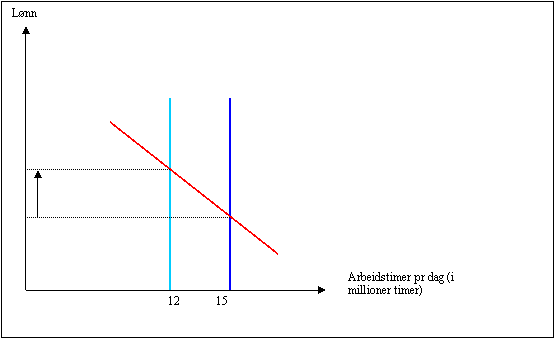
Lønnen vil gå opp som følge av redusert arbeidstilbud.

b) Når lønnen blir høyere, så vil arbeidsgivere substituere seg bort fra den relativt dyre innsatsfaktoren, og mot for eksempel kapital. Dette kan vises som i figuren under.

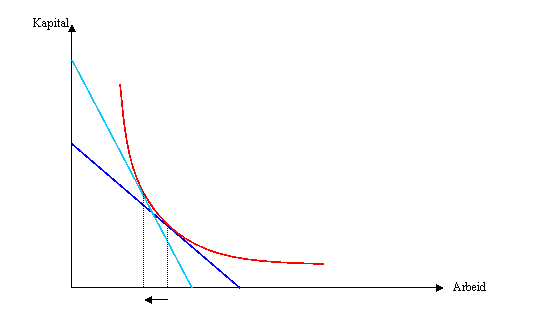
Som figuren viser så vil en kostnadsminimerende bedrift redusere etterspørselen etter arbeid når lønnen stiger (illustrert ved den lyseblå isokostlinjen).

Oppgave 3 (Vekt: 25 %)

Oppgavetekst

En monopolist står overfor en grensekostnadsfunksjon gitt ved:

Etterspørselen i markedet er gitt ved: .

a) Beregn pris og produsert kvantum i markedet.

b) Hvor stor er monopolistens produsentoverskudd?

c) Hvis monopolisten av en eller annen grunn skulle ønske å oppføre seg som en bedrift i frikonkurranse, hva vil da likevektskvantum, likevektspris og produsentoverskudd bli?

d) Hva blir velferdstapet ved monopol?

Løsningsforslag

Svarene er gitt både i desimaltall og som brøk (noe som er lettere å regne med).

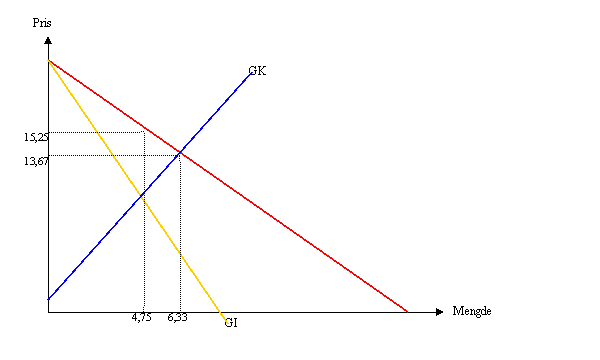
a) Pris = 15,25 (eller 61/4), mengde = 4,75 (eller 19/4)

b) Produsentoverskuddet = 45,125 (eller 361/8)

c) Pris = 13,67 (eller 41/3), Mengde = 6,33 (eller 19/3), Produsentoverskuddet = 40,11 (eller 361/9).

d) Velferdstapet ved monopol = 3,76 (eller 361/96)

Løsningsforslag eksamensoppgave i mikroøkonomi ved HiMolde 6. januar 2006 (kontinuasjonseksamen)

Oppgavetekst

Anta at en bedrift produserer en vare ved hjelp av to produksjonsfaktorer. Anta videre at vi har fullkommen konkurranse både på faktormarkedet og produktmarkedet.

a) Forklar hvorfor deler av bedriftens grensekostnadskurve er lik bedriftens tilbudskurve.

b) Hva skjer med tilbudt (produsert) mengde og overskuddet dersom prisen på varen øker?

c) Hva skjer med produsert mengde og etterspørselen etter de to produksjonsfaktorene dersom prisen på den ene produksjonsfaktoren øker?

Løsningsforslag

a) Her er det meningen du skal benytte deg av tilpasningen for en profittmaksimerende produsent. Generelt vil en slik produsent tilpasse seg der grenseinntekt er lik grensekostnad. Grenseinntekten for en produsent i frikonkurranse er prisen på godet hun produserer. Altså skal pris være lik grensekostnad i tilpasningspunktet. Med dette som utgangspunkt må du si noe om kostnadskurvene for produsenten. Det er ikke meningen at du herr skal utlede alle de forskjellige kostnadskurvene, men det er fint om du forklarer hovedmomentene og tegner grafene. Da skal du ha en figur slik:

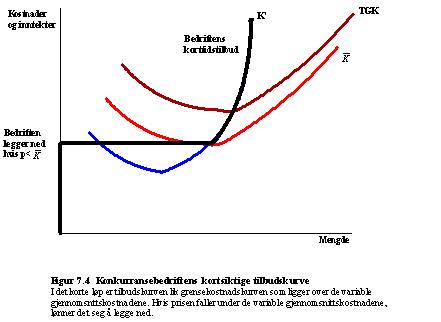
Her må du argumentere for hvorfor den svarte kurven blir produsentens tilbudskurve i det korte løp. For en pris høyere enn gjennomsnittskostnaden tilpasser produsenten seg der prisen er lik grensekostnaden. Det vil si at tilpasningen blir langs grensekostnadskurven for p > . I det lange løp må bedriften dekke også de faste kostnadene, derfor må prisen nå være større enn de totale gjennomsnittskostnadene TGK.

b) Prisen er i utgangspunktet p₀. Da tilbys kvantum X₀. Overskuddet er da (pris)x(kvantum) – (gjennomsnittskostnad)x(kvantum), det vil si pris – gjennomsnittskostnad)x(kvantum), eller med symboler: (p₀ – ₀)X₀, hvor ₀ = bX₁. Det svarer til arealet p₀abc. Prisen stiger så til p₁. Da øker tilbudet til X₁. Det nye overskuddet blir nå arealet p₁def. Du ser lett at det nye overskuddet er større enn det gamle. Konklusjon: Både tilbudt mengde og overskudd øker når prisen øker.

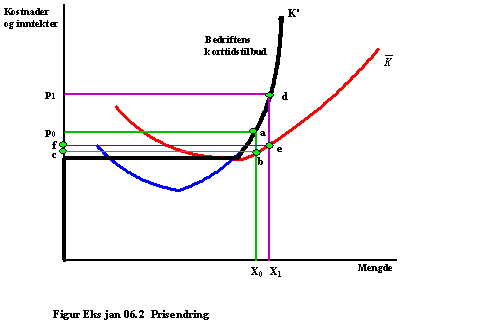
c) Her må du gå ut fra at bedriftens kostnader K er konstant i analysen. Det samme er produktprisen. Da får du følgende figur:

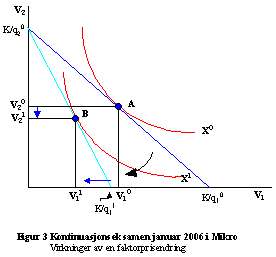
Utgangspunktet er A hvor forbruket av innsatsfaktorer er henholdsvis V₁⁰ og V₂⁰, produktmengden er X⁰, de totale kostnader er K og faktorprisene er henholdsvis q₁⁰ og q₂⁰. Prisen på faktor 1 øker så til q₁¹, noe som får kostnadslinjen til å svinge innover rundt punktet K/q₂⁰. Ny tilpasning blir i B, hvor produktmengden nå er X¹ < X⁰ Samtidig ser vi av figuren at bruken av faktor 1 går ned fra V₁⁰ til V₁¹ mens bruken av faktor 2 øker fra V₂⁰ til V₂¹.

Konklusjon: Bruk av innsatsfaktor 1 (hvis pris øker) går ned, mens bruk av faktor 2 går opp. (Jeg gjør oppmerksom på at det også er mulig at bruken av faktor 2 går ned, du kan jo prøve å tegne figur for det.) Produktmengden går opp.

Løsningsforslag til eksamen i mikroøkonomi ved HSM 9. mai 2006

Oppgavetekst

Myndighetene ønsker å redusere bensinprisen. Det kan de gjøre ved enten å sette en effektiv maksimumspris (innføre et effektivt pristak) eller ved å redusere avgiften på bensin.

a) Sammenlign velferdsvirkningene av de to måtene å redusere bensinprisen på.

b) Hva vil du anbefale myndighetene å gjøre. Begrunn!

(En liten hjelp: Husk å sette pristaket (maksimumsprisen) lik pris etter avgiftsreduksjonen.)

Løsningsforslag

Meningen er i det store og det hele at studentene skal sammenligne de to figurene nedenfor

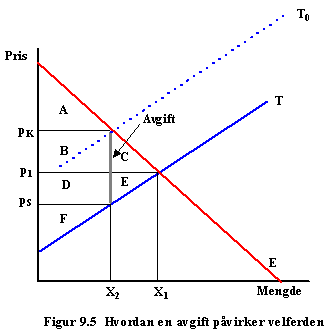
Men dette er figurene fra boken. Jeg har her lagt til den ”opprinnelige” tilbudskurven (før innføring av avgift). Utgangspunktet nå er likevekt i skjæringen mellom stiplet tilbudskurve og e-kurven med omsatt kvantum X₂ og konsumentpris p_K. Så reduseres avgiften. Det enkleste er å ta den helt bort. Da får vi det ”omvendte” resonnement av det som følger figur 9.5 i boken. Ny likevektspris blir p₁. De gode studentene bør da kunne vise velferdsvirkningen med en tabell som er ”motsatt” av tabell 9.1 i boken:

Velferdsvirkninger av en avgiftsreduksjon (fjerning av avgift)
	Før avgiftsreduksjon	Etter avgiftsred.	Virkning av avgiftsred.
Konsumentoverskudd	A	A + B + C	B + C
Produsentoverskudd	F	D + E + F	D + E
Avgiftsbeløp	B + D	0	–(B + D)
Samfunnsøkonomisk overskudd	A + B + D + F	A + B + C + D + E + F	C + E

Konklusjon: alle ”overskuddene” går opp både konsument-, produsent- og sosialt overskudd, Det er ikke lenger nødvendig med administrasjon og inndriving av avgiften.

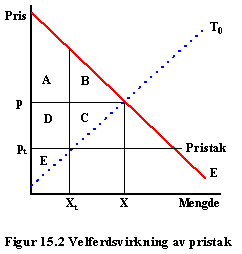
Pristak diskuteres med utgangspunkt i figur 15.2, hvor T-kurven er den samme som den stiplete t-kurven i figur 9.5 (slik jeg har tegnet den i figur 9.5). Her bør studentene tegne figuren slik at p_t = p_1. Analysen følger nå boken side 373–374. Konklusjonen nå er at omsetningen går ned, det gjør også alle ”overskuddene”, det blir et etterpørselsoverskudd, og en eller annen form for rasjonering må innføres eller etableres. Administrasjonskostnader påløper.

Anbefalingen, ut fra økonomisk teori bør være klar: avgiftsreduksjon fremfor pristak.